An Explanation of Summation Notation With Examples

First published 1st September 2023 Robin James

Find us on Facebook Follow us on Twitter

Summation notation is a concise mathematical shorthand used to write the sum of a sequence of terms. It uses the Greek letter sigma ‘∑’ as its symbol, which denotes summation. This notation allows mathematicians to express lengthy and complex series in a compact and explicit format.

Sigma notation finds extensive use in calculus where it helps represent and evaluate limits, derivatives, and integrals. This article will delve deep into summation notation, exploring its definition, properties, and application. We will provide many examples for our readers to solidify this concept.

What is Summation Notation?

Summation notation provides a concise way to express the addition of multiple terms that follow a specific pattern without having to write them all out explicitly. The notation is particularly useful when dealing with large or infinite sequences.

The general form of summation notation is as follows:

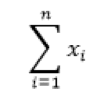
Where;

• Σ (capital sigma) represents the summation symbol.
• The expression below the sigma indicates the starting point of the summation.
• The expression above the sigma indicates the ending point of the summation.
• The variable used in the expression and its range of values are specified.
• The term being summed is written to the right of the sigma.

Steps for Writing a Sequence’s Sum Using Summation Notation

Writing the sum of a sequence of terms in the form of summation notation by the addition of all the terms in a simple, concise, and standard form of the function. To write the series of numbers in the standard summation notation follow the below steps.

1. Identify the Sequence:

Understand the sequence of terms you want to sum.

2. Determine the upper and lower limit:

Decide on the range over which you want to perform the summation. Selecting the base and index values for the summation notation. By allocating particular variables and establishing the value of the integers, these points are defined.

3. Select a Variable:

Select the variable to show the terms of the sequence in generating the general form of summation notation. Common choices for the variable are “i, j, and k” in the lowercase letters.

4. Write the Sigma Notation:

Use the Sigma “∑” notation symbol to represent the sum of the terms. The general form of the summation notation is written as.

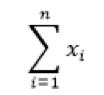
Replace the components of the notation with the appropriate information from steps 2 and 3. This expression represents the terms of the sequence you are summing.

Steps to Expand Summation Notation

Steps are given below to explain how to expand summation notation:

Identify the range and the variable used in the summation.
Write down the expression being summed.
Substitute the values of the variable into the expression for each term within the range.
Write down a positive symbol between all founded terms and sum up them.

By following these steps, you can expand most summation notations to understand the sequences or series they represent. Additionally, if you’re looking for a quick solution, you can use a summation calculator available online.

Summation notation properties

Here are some key properties of Sigma notation.

Linearity of Summation notation:

The linearity of the summation notation for the two sequences is defined if the two sequences ∑ (cᵢ) and ∑ (dᵢ) and “a or b” are two real constants. Then it is shown as,

∑ (a cᵢ ± b dᵢ) = a ∑ (cᵢ) ± b ∑ (dᵢ)

Splitting a Sum of two summation notation:

Distributive law of the summation notation into two separate summations as below.

∑ (cᵢ + dᵢ) = ∑ (cᵢ) + ∑ (dᵢ)

Changing the Index:

You can change the index of summation without changing the result.

∑ (cᵢ) = ∑ (cⱼ)

Re-indexing:

You can shift the index of summation without changing the result.

∑ (cᵢ) = ∑ (cᵢ₊ₖ). Where k is a constant.

Switching the Order of Summation

For certain types of sequences, you can switch the order of summation.

∑ (∑ (cᵢ)) = ∑ (∑ (cⱼ)). Where j is a function of i.

Solved Examples of Summation Notation

Here are solved examples that explain how to express sequences and expanding functions using summation notation.

Example 1:

Write the series of the number in the summation notation.

2 + 4 + 6 + 8 + 10 + 12 + 14.

Solution:

Step 1:

Identify the Sequence of the numbers.

We noted that the sequence of the number in this example is the set of even numbers starting from 2 and increasing “2” in the coming of every next number.

Step 2:

Find out the Upper and Lower Limits of the summation notation.

The series starts with the number 2 and ends with the number 14.

The lower limit i = 1
The upper limit n = 7

Step 3: Select a Variable

Choose the variable i to represent the terms of the sequence as they change.

Step 4: Write the Sigma Notation

Using the information from steps 2 and 3, we can write the sigma notation for this series:

∑ i = 1 7 2i
∴ 2 + 4 + 6 + 8 + 10 + 12 + 14 = ∑ i = 1 7 2i

Example 2:

Expand the following summation notation:

∑ i = 1 5 (–1)i × 2i

Solution:

Step 1:

Evaluate the terms using the series function.

Put “i = 1”.
(–1)1 × 2(1) = – 2

Put “i = 2”.
(–1)2 × 2(2) = 4

Put “i = 3”.
(–1)3 × 2(3) = – 6

Put “i = 4”.
(–1)4 × 2(4) = 8

Put “i = 5”.
(–1)5 × 2(5) = – 10

Step 2:

Add up the terms the all terms.

∴ ∑ i = 1 5 (–1)i × 2i = –2 + 4 – 6 + 8 – 10 = –6

Conclusion

In this article, a basic definition with steps of summation to determine the sequence of summation notation is discussed. Moreover, discussed the properties of the summation notation and for a better understanding of the summation solved the examples with detailed explanations.